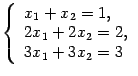 |
(15.4) |
Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных. Например, система из трех уравнений с двумя неизвестными
Ответ на вопрос о совместности произвольной системы уравнений (15.1) дает приведенная ниже теорема.
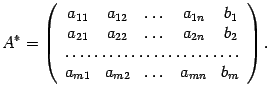
Пусть ![]() .
Предположим, что
.
Предположим, что ![]() ,
, ![]() . Тогда в матрице
. Тогда в матрице ![]() есть линейно независимая система из
есть линейно независимая система из ![]() столбцов. Среди этих столбцов может быть только один, не
принадлежащий матрице
столбцов. Среди этих столбцов может быть только один, не
принадлежащий матрице ![]() . Тогда
подсистема остальных
. Тогда
подсистема остальных ![]() столбцов,
принадлежащих матрице
столбцов,
принадлежащих матрице ![]() , должна быть
линейно независимой. Следовательно,
, должна быть
линейно независимой. Следовательно, ![]() .
Получили противоречие. Предположение, что
.
Получили противоречие. Предположение, что ![]() , неверно.
, неверно.
1. Пусть система имеет решение. Покажем, что ![]() .
.
Пусть набор чисел ![]() является
решением системы. Обозначим через
является
решением системы. Обозначим через ![]()
![]() -ый столбец матрицы
-ый столбец матрицы ![]() ,
, ![]() . Тогда
. Тогда ![]() , то есть
столбец свободных членов является линейной комбинацией столбцов матрицы
, то есть
столбец свободных членов является линейной комбинацией столбцов матрицы ![]() . Пусть
. Пусть ![]() .
Предположим, что
.
Предположим, что ![]() . Тогда по
предложению 15.1
. Тогда по
предложению 15.1 ![]() . Выберем
в
. Выберем
в ![]() базисный минор
базисный минор ![]() . Он имеет порядок
. Он имеет порядок ![]() . Столбец
. Столбец ![]() свободных
членов обязан проходить через этот минор, иначе он будет базисным минором
матрицы
свободных
членов обязан проходить через этот минор, иначе он будет базисным минором
матрицы ![]() . Столбец свободных членов в миноре
. Столбец свободных членов в миноре ![]() является линейной комбинацией столбцов матрицы
является линейной комбинацией столбцов матрицы
![]() . В силу свойств определителя ( предложения 14.13, 14.18)
. В силу свойств определителя ( предложения 14.13, 14.18) ![]() , где
, где
![]() -- определитель, который получается
из минора
-- определитель, который получается
из минора ![]() заменой
столбца свободных членов на столбец
заменой
столбца свободных членов на столбец ![]() . Если
столбец
. Если
столбец ![]() проходил
через минор
проходил
через минор ![]() , то в
, то в ![]() , будет два одинаковых столбца и, следовательно,
, будет два одинаковых столбца и, следовательно,
![]() . Если столбец
. Если столбец ![]() не проходил через минор
не проходил через минор ![]() ,
то
,
то ![]() будет отличаться от минора порядка
будет отличаться от минора порядка ![]() матрицы
матрицы ![]() только
порядком столбцов. Так как
только
порядком столбцов. Так как ![]() , то
, то ![]() . Таким образом,
. Таким образом, ![]() , что
противоречит определению базисного минора. Значит, предположение, что
, что
противоречит определению базисного минора. Значит, предположение, что ![]() , неверно.
, неверно.
2. Пусть ![]() . Покажем,
что система имеет решение. Так как
. Покажем,
что система имеет решение. Так как ![]() , то
базисный минор
, то
базисный минор ![]() матрицы
матрицы
![]() является базисным минором матрицы
является базисным минором матрицы ![]() . Пусть через минор
. Пусть через минор ![]() проходят столбцы
проходят столбцы ![]() . Тогда
по теореме о базисном миноре в матрице
. Тогда
по теореме о базисном миноре в матрице ![]() столбец свободных членов является линейной комбинацией
указанных столбцов:
столбец свободных членов является линейной комбинацией
указанных столбцов:
В рассмотренной выше системе (15.4) ![]() , и
система является совместной. В системе (15.5)
, и
система является совместной. В системе (15.5) ![]() ,
, ![]() , и
система является несовместной.
, и
система является несовместной.